Craig uses probability calculus to attempt to refute Ehrman’s claim that historians “cannot say that the explanation which is inherently the most improbable is probable” (whether or not he succeeded is up to you). For a summary of Ehrman's argument against the resurrection, see: http://honestsearchfortruth.blogspot.com/2011/09/can-miracle-ever-be-best-explanation.html
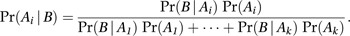 Don’t get intimidated by this big equation! There is a simple way to break it down.
Don’t get intimidated by this big equation! There is a simple way to break it down.
The best way to explain this will be to use an example. We will make it simple- only two events- A1 and A2.
Keep in mind that picking Coin X corresponds to the event “A1.” Picking Coin Y corresponds to “A2.”
Now, let’s make B the ‘event’ of obtaining heads after flipping the coin that Larry randomly selects.
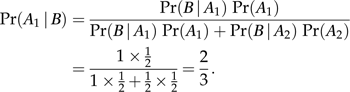
What this mathematical thingy is saying is this: “given that ‘heads’ was the outcome, the probability that it was the double-headed coin that was flipped is 2/3.” (science.jrank.org)
Or rather, same example, but let’s do it where we are finding Pr(A2|B) instead of Pr(A1|B).
Now we plug in our numbers:
Pr(A2|B)= ½ x ½
(½ x ½) + (1 x ½)
And after we do some fun math we come out with Pr(A2|B)= 1/3
This means: Given that ‘heads’ was obtained, the probability that it was Coin 2 that was tossed is 1/3.
From our first two examples, we now know that if the event that occurs is obtaining heads (or B=’the event of obtaining heads), that the probability that it was Coin 1 that was flipped is 2/3, and the probability that it was Coin 2 that was flipped is 1/3.
-----------------------------------------------------------------------------------
Ok time for a break! NOT. TIME FOR ANOTHER EXAMPLE!!! MUAHAHAHAHAAHAAAA!
Anyway,iIf you are like me, you NEED this many examples to understand these principles. In addition, IF YOU WANT TO KNOW WHETHER OR NOT IT IS PROBABLE THAT JESUS ROSE FROM THE DEAD, YOU NEED TO UNDERSTAND BAYE’S THEOREM. And I’m going to make it as easy as possible for you! I'm doing all the leg work!
----------------------------------------------------------------------------------
Ok, same example as before, but we are going to make C the event of obtaining ‘tails’ instead of using B.
So, given that ‘tails’ was obtained, what is the probability that it was Coin 1 that was tossed?
Our mathematical thingy:
Pr(A1|C)= Pr(C|A1) Pr(A1)
Pr(C|A1) Pr(A1) + Pr(C|A2) Pr(A2)
Now we plug in the numbers:
Pr(A1|C)= 0 x ½
(0 x ½) + (½ x ½)
This means: Given that ‘tails’ was obtained, the probability that it was Coin 1 that was tossed is 0.
*This example is especially useful because you can use your intuition to find the answer without using math- ‘tails’ cannot be obtained from flipped a coin with heads on both sides. By relating your intuition to the math, you can increase your understanding of probabilities!
-----------------------------------------------------------------------------
WHO’S READY FOR ONE MORE EXAMPLE? Well, I’ve only been studying, writing, and trying to make this crazy math stuff understandable for the past 6 hours of my Saturday morning. Might as well be thorough.
This last example should be ridiculously easy if you read the first three.
Same example, but let’s see what the probability of Coin 2 being tossed is if the result is ‘tails.'
Pr(C|A2) Pr(A2) + Pr(C|A1) Pr(A1)
Pr(A2|C)= ½ x ½
(½ x ½) + (0 x ½)
This means: Given that ‘tails’ was obtained, the probability that it was Coin 1 that was tossed is 1 (or 100%).
If you managed to make it this far in this post, the next time I see you, I WILL give you a hug. If you don’t want to be hugged, just tell me that you didn’t read the last word or two. Otherwise I WILL hug you.
In the debate, Craig had severe time limitations and could not explain the probability calculus he used enough for most people to understand what the heck he was talking about. Out here in the real world, however, we have as much time as we would like! This means that I will be spending my Saturday morning learning about and explaining the relevant topics in probability calculus for you. This is necessary if we want to make a decision as to whether Craig, Ehrman, or neither of them is correct on the historicity resurrection! To know whether or not Jesus rose from the dead, you need to know a little probability calculus.
I promise that I will only share the math that is absolutely necessary for understanding! Don’t be intimidated by the subject material of this post- it is pretty easy if you attack it with patience and confidence!
In addition, if promise to help anyone who is willing to learn with this topic! Comment, email, call, or coffee!
---------------------------------------------------------------------------
**But first, thank you to science.jrank.org!!! (the website from which I obtained my knowledge) <a href="http://science.jrank.org/pages/51901/prior-probability.html">prior probability</a>
---------------------------------------------------------------------------
Here are two kinds of probabilities: A prior probability and a posterior probability.- Prior probability- “The probability attached to an event before certain data are obtained.”
- Posterior probability- “the probability attached to it after the data are obtained.”
Because the information on the resurrection of Jesus has already been obtained, we are looking at a posterior probability.
To find a posterior probability, we use Baye’s Theorem:
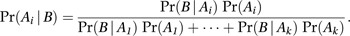
Pr(Ai|B) is the thing we are trying to find. It is the probability of an event, (Ai), happening with respect to other events B. A1 is one event, A2 is another event, A3 is another event, and we can just keep on adding as many events as we want. The total number of events we have in our probability is equal to K.
The best way to explain this will be to use an example. We will make it simple- only two events- A1 and A2.
- Let’s make A1 the tossing of a double sided coin- both sides are heads. We will call this coin “Coin X. ” The probability of getting ‘heads’ when tossing Coin X is 100%. Event probability: 100%.
- Let’s make A2 the tossing of a normal coin with heads on one side and tails on the other. We will call this coin “Coin Y.” The probability of getting ‘heads’ when tossing Coin Y is 50%. Event probability: 50%
Keep in mind that picking Coin X corresponds to the event “A1.” Picking Coin Y corresponds to “A2.”
The way to say that “the probability of Larry picking Coin 1 is 50%” is: Pr(A1)=1/2
The way to say that “the probability of Larry picking Coin 2 is 50%” is: Pr(A2)=1/2
Now, let’s make B the ‘event’ of obtaining heads after flipping the coin that Larry randomly selects.
- If Larry picks Coin 1, the probability of obtaining heads is 100%, or Pr(B|A1)=1
- If Larry picks Coin 2, the probability of obtaining heads is 50%, or Pr(B|A2)=1/2
We are reading to see the whole mathematical formula for our example.
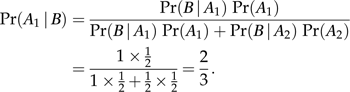
What this mathematical thingy is saying is this: “given that ‘heads’ was the outcome, the probability that it was the double-headed coin that was flipped is 2/3.” (science.jrank.org)
----------------------------------------------------------------------------------------------------
Know what I think it is time for? ANOTHER EXAMPLE!!!
Summary of Heads Example:
Pr(A1) = 1/2
Pr(A2) = 1/2
Pr(B|A1) = 1
Pr(B|A2) = 1/2
So, given that ‘heads’ was obtained, what is the probability that it was Coin 2 that was tossed?
Here is the mathymajigger:
Pr(A2|B)= Pr(B|A2) Pr(A2)
Pr(B|A2) Pr(A2) + Pr(B|A1) Pr(A1)Now we plug in our numbers:
Pr(A2|B)= ½ x ½
(½ x ½) + (1 x ½)
And after we do some fun math we come out with Pr(A2|B)= 1/3
This means: Given that ‘heads’ was obtained, the probability that it was Coin 2 that was tossed is 1/3.
From our first two examples, we now know that if the event that occurs is obtaining heads (or B=’the event of obtaining heads), that the probability that it was Coin 1 that was flipped is 2/3, and the probability that it was Coin 2 that was flipped is 1/3.
-----------------------------------------------------------------------------------
Ok time for a break! NOT. TIME FOR ANOTHER EXAMPLE!!! MUAHAHAHAHAAHAAAA!
It seems like I woke up this morning and thought “I wonder what blog post I could write to scare off the most people, give the highest number of people headaches, and discourage basically everyone to never read anything Josh writes again? Oh! I know! I’ll do an excruciatingly long post on PROBABILITY CALCULUS!!! And then I’ll give them… As many examples as they will need to actually understand what I’m saying...”
Anyway,iIf you are like me, you NEED this many examples to understand these principles. In addition, IF YOU WANT TO KNOW WHETHER OR NOT IT IS PROBABLE THAT JESUS ROSE FROM THE DEAD, YOU NEED TO UNDERSTAND BAYE’S THEOREM. And I’m going to make it as easy as possible for you! I'm doing all the leg work!
----------------------------------------------------------------------------------
Ok, same example as before, but we are going to make C the event of obtaining ‘tails’ instead of using B.
So, given that ‘tails’ was obtained, what is the probability that it was Coin 1 that was tossed?
- Let’s make A1 the tossing of a double sided coin- both sides are heads. The probability of getting ‘tails’ when tossing Coin X is 0%. Event probability: 0%.
- Let’s make A2 the tossing of a normal coin with heads on one side and tails on the other. The probability of getting ‘tails' when tossing Coin Y is 50%. Event probability: 50%
- The probability of Larry picking Coin 1 is 50%: Pr(A1)=1/2
- The probability of Larry picking Coin 2 is 50%: Pr(A2)=1/2
- If Larry picks Coin 1, the probability of obtaining tails is 0%, or Pr(C|A1)=0
- If Larry picks Coin 2, the probability of obtaining tails is 50%, or Pr(C|A2)=1/2
Summary of Tails Example:
Pr(A1) = 1/2
Pr(A2) = 1/2
Pr(B|A1) = 0
Pr(B|A2) = 1/2
Our mathematical thingy:
Pr(A1|C)= Pr(C|A1) Pr(A1)
Pr(C|A1) Pr(A1) + Pr(C|A2) Pr(A2)
Now we plug in the numbers:
Pr(A1|C)= 0 x ½
(0 x ½) + (½ x ½)
This means: Given that ‘tails’ was obtained, the probability that it was Coin 1 that was tossed is 0.
*This example is especially useful because you can use your intuition to find the answer without using math- ‘tails’ cannot be obtained from flipped a coin with heads on both sides. By relating your intuition to the math, you can increase your understanding of probabilities!
-----------------------------------------------------------------------------
WHO’S READY FOR ONE MORE EXAMPLE? Well, I’ve only been studying, writing, and trying to make this crazy math stuff understandable for the past 6 hours of my Saturday morning. Might as well be thorough.
This last example should be ridiculously easy if you read the first three.
Same example, but let’s see what the probability of Coin 2 being tossed is if the result is ‘tails.'
Summary of Tails Example:
Pr(A1) = 1/2
Pr(A2) = 1/2
Pr(B|A1) = 0
Pr(B|A2) = 1/2
And the summary in english:
- The probability of Larry picking Coin 1 is 50%: Pr(A1)=1/2
- The probability of Larry picking Coin 2 is 50%: Pr(A2)=1/2
- If Larry picks Coin 1, the probability of obtaining tails is 0%, or Pr(C|A1)=0
- If Larry picks Coin 2, the probability of obtaining tails is 50%, or Pr(C|A2)=1/2
Pr(C|A2) Pr(A2) + Pr(C|A1) Pr(A1)
Pr(A2|C)= ½ x ½
(½ x ½) + (0 x ½)
This means: Given that ‘tails’ was obtained, the probability that it was Coin 1 that was tossed is 1 (or 100%).
If you managed to make it this far in this post, the next time I see you, I WILL give you a hug. If you don’t want to be hugged, just tell me that you didn’t read the last word or two. Otherwise I WILL hug you.
So, what does this have to do with the resurrection of Jesus? Check out my next post on Craig’s rebuttal of Ehrman’s argument against the resurrection of Jesus. Now that you are equipped with ‘the sword of probability calculus,’ you will be able to understand what the heck William Lane Craig is actually talking about!
For more analysis of probability, and a greater focus on the implications for the Craig-Ehrman debate, check out this post by neo the philosopher.
For more analysis of probability, and a greater focus on the implications for the Craig-Ehrman debate, check out this post by neo the philosopher.

The math in your examples looks correct, but there is one error that should be addressed. It's minor but crucial for someone who isn't familiar with this.
ReplyDeleteIn your explanation of the theorem, you indicated that Pr(Ai|B) is "the probability of an event, B, happening with respect to other events (Ai)." Pr(Ai|B) is the probability of Ai occurring given that B occurs (the opposite of what you said). You explained the math and the meaning of the math correctly in all of your examples, so you clearly understood the theorem, but this may be a point of confusion for someone who is new to probability.
Hi!
ReplyDeleteSorry it took me so long to respond to your comment!
Thank you for taking the time to read my post and point out my silly mistake. I'll get that corrected asap.
Hope you continue to enjoy reading!
Great stuff, I've been bashing my head trying to work out the best way to point out the misuse of Bayesian inference by Craig in the Ehrman debate. I think you came pretty close (although you might have had a different objective).
ReplyDeleteAnyways, please point out that Craig didn't invent this, he got it from Richard Swinburne. Getting it from Swinburne doesn't make it any more valid, pointing out the origin highlights that Craig doesn't only attempt to confuse, he also steals his material (oops, did I say "steals", I meant to say "borrows").
It seems we have other lines of common interest, I also had a look at his ontological argument (albeit in a few more words).
neopolitan (http://neophilosophical.blogspot.com)
Hi neo!
ReplyDeleteThanks a lot for your comment. My objective for this post was a mere attempt at mathematical education. However, it would be a good idea for me to take the next step and explain how this applies to the Craig vs Ehrman debate.
Also, thanks for the tip on Swinburne. Credit where credit is due! I cqtms'd (chuckled-quietly-to-myself) (what most people mean when they say 'lol') at your quip about stea 'borrowing' material.
I took a trip over to your blog just now and found out that we do indeed have many common interests. I appreciate the level of detail you put in to all of your posts (the 4 I have read so far anyway). Many of mine are on the shorter side because I'm trying to target a more generalized crowd. However, I have really enjoyed the amount of ground you cover by being totally comprehensive.
I think I'll start making my posts more thorough like yours, even if it does make them a bit harder to read (obviously I'm not talking about this one- this one was plenty hard to read). Got to keep the quality high!
I look forward to reading more of your work, and hearing feedback from you on mine.
-Josh the Searcher
Thank you so much for this. I've been searching for a couple of hours for somewhere that gives a basic breakdown of the concept of the math used in the Craig/Ehrman debate. All I managed to find were a lot of threads where it was being discussed but not really explained. I really appreciate it. Your examples were explained on the exact level that I needed them explained.
ReplyDeleteI would still appreciate a little clarification though (I know, right?) Given that we know the result is heads, I'm confused as to how coin 1 can be said to be the more probable cause. That the probability of coin 1 being chosen is greater than coin 2 appears to be based on the fact that coin 2 *can* return a different result. However we know that the result isn't the alternative result and so the probability of which coin caused it must still be 50/50. Just because it is less likely *to* it doesn't mean that it less likely *did*. Or does it? Or am I missing something?
Great blog. I've only read this post and I've immediately added it to my RSS feed.